!수학 없는🙀! Stable Diffusion에 대한 이해.

자, Stable Diffusion이 뭔지 검색해 봤는데, 수식이 넘쳐나서 당황하신 분들을 환영합니다.

정말 코딱지만한 딥러닝, 머신러닝 지식만 있다면,
여러분은 이 글을 읽고 Stable Diffusion의 원리를 대충 파악할 수 있습니다.

그럼 시작하겠습니다!

시자아아아아아아아아아아아아아악

❓Diffusion은 뭘까 

Stable Diffusion에 앞서, Diffusion이 뭔지 알고 넘어가 보자.

 

보통 물에 잉크를 한 방울 똑! 떨어뜨리면

점점 퍼져나가다가(확산하다가) 결국 균일하게 퍼지게 될 것이다.

그리고 확산은 영어로 Diffusion이다.

 

잉크의 확산(Diffusion)

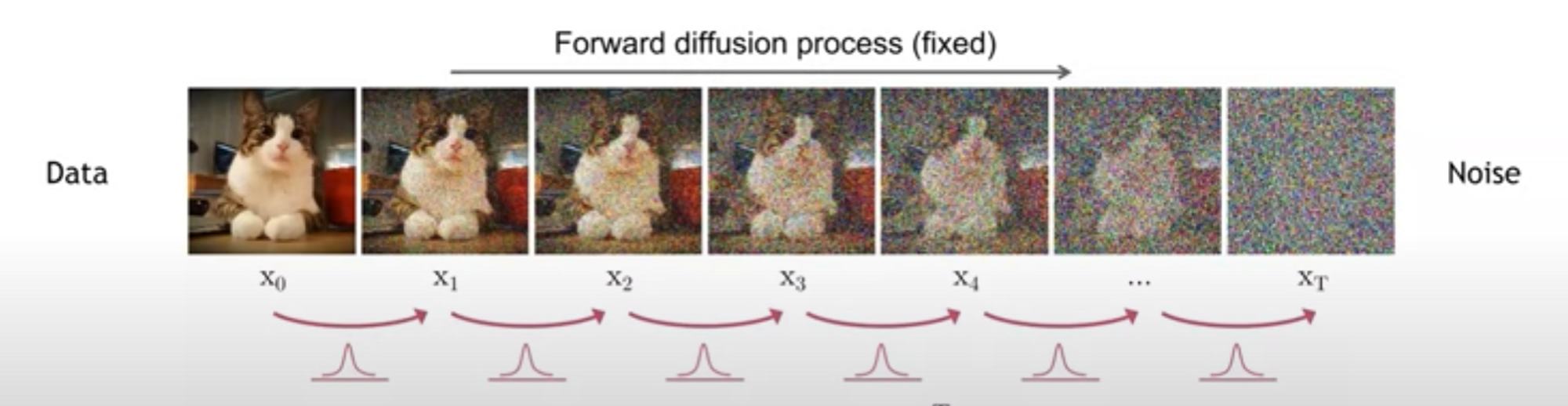
마찬가지로, 이미지(데이터)에 노이즈를 추가하여 점차 완전히 노이즈로 가는 과정을 Diffusion 과정이라고 한다.

그리고, 그 반대 과정을 통해서 "랜덤 한 노이즈"로부터 "이미지"를 추측하는 것을 "De-noising"이라고 한다.

• 반대 과정을 학습하는 방법은 아래에서 설명.
• 그럼, 결국 나중에는 "노이즈"만 있어도 "이미지"를 만들 수 있게 된다.
• Stable Diffusion이라는 이름은, 학습이 Stable, 안정적이 여서도 있겠지만, Stable이라는 회사에서 만들었다. 

 

💡 모델 구조 및 원리 분석

모델의 대략적인 구조도. 빨간색 ➡️ 노란색 ➡️ 파란색 순서로 설명할 것이다.

Denoiser (U-Net)

자, 아까 말했던 "De-Noising"을 하는 모델이 Denoiser이다. 

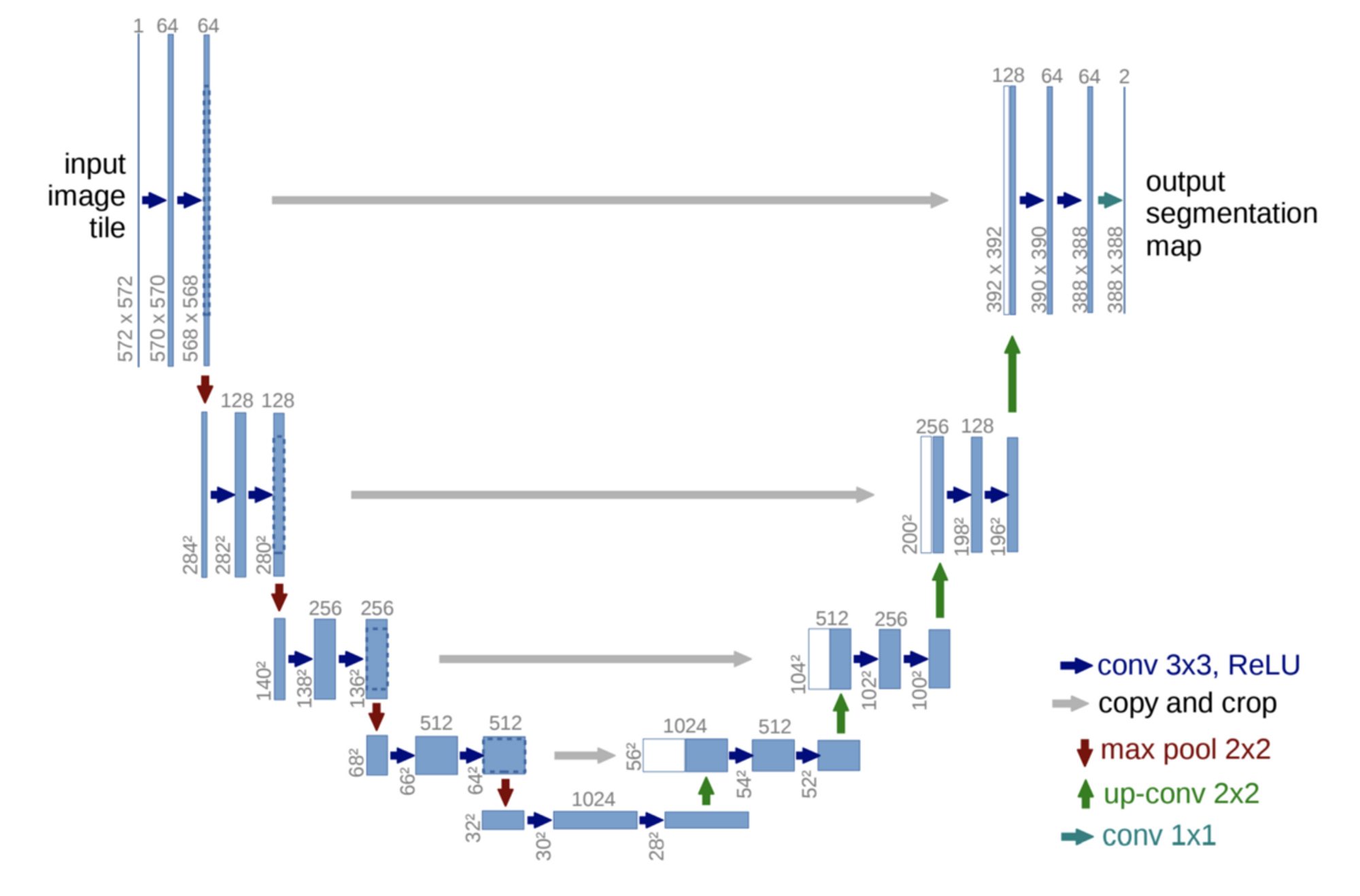
근데 별칭이 U-Net이네? 왜 U-Net일까?

- 아래처럼 생겼기 때문에 U-Net이라고 부름.

- TMI) 물론 아래 이미지와는 조금 다르게, 2d Convolution만 들어간 것이 아니라, self attention 및 cross attention layer가 들어감.

U-Net 원 논문 구조도.

📚 필수 배경 지식
"딥러닝 모델은 이미지-라벨(Input-Output, x-y)의 데이터셋으로 학습시키면, 이미지를 주었을 때 라벨을 예측할 수 있다."

설명하자면 길어지기 때문에, 모르겠다면, 그냥 마음으로 공감해보자.

놀라운 사실은, 우리에게 이미지만 있다면, 우리는 랜덤한 노이즈를 생성하여 "노이즈가 조금 추가된 이미지"를 만들 수 있다.

➡️ 이것이 일종의 학습 데이터 쌍이 된다.

노이즈가 낀 이미지를 주면, 추가된 노이즈를 예측하는 U-Net(Denoiser).

• 노이즈가 추가된 이미지와, 노이즈의 정도를 주면 (Input).
• 노이즈를 예측(Output)하여, 이미지에서 빼낸다 → Denoise!
• 완전한 노이즈에서, 노이즈를 반복적으로 예측하여 빼내면, 이미지가 생성되는 방식.

노이즈 낀 이미지 ➡️ 노이즈 예측해서 빼기 ➡️ 노이즈가 조금 빠진 이미지 ➡️ 노이즈 또 예측해서 빼기...

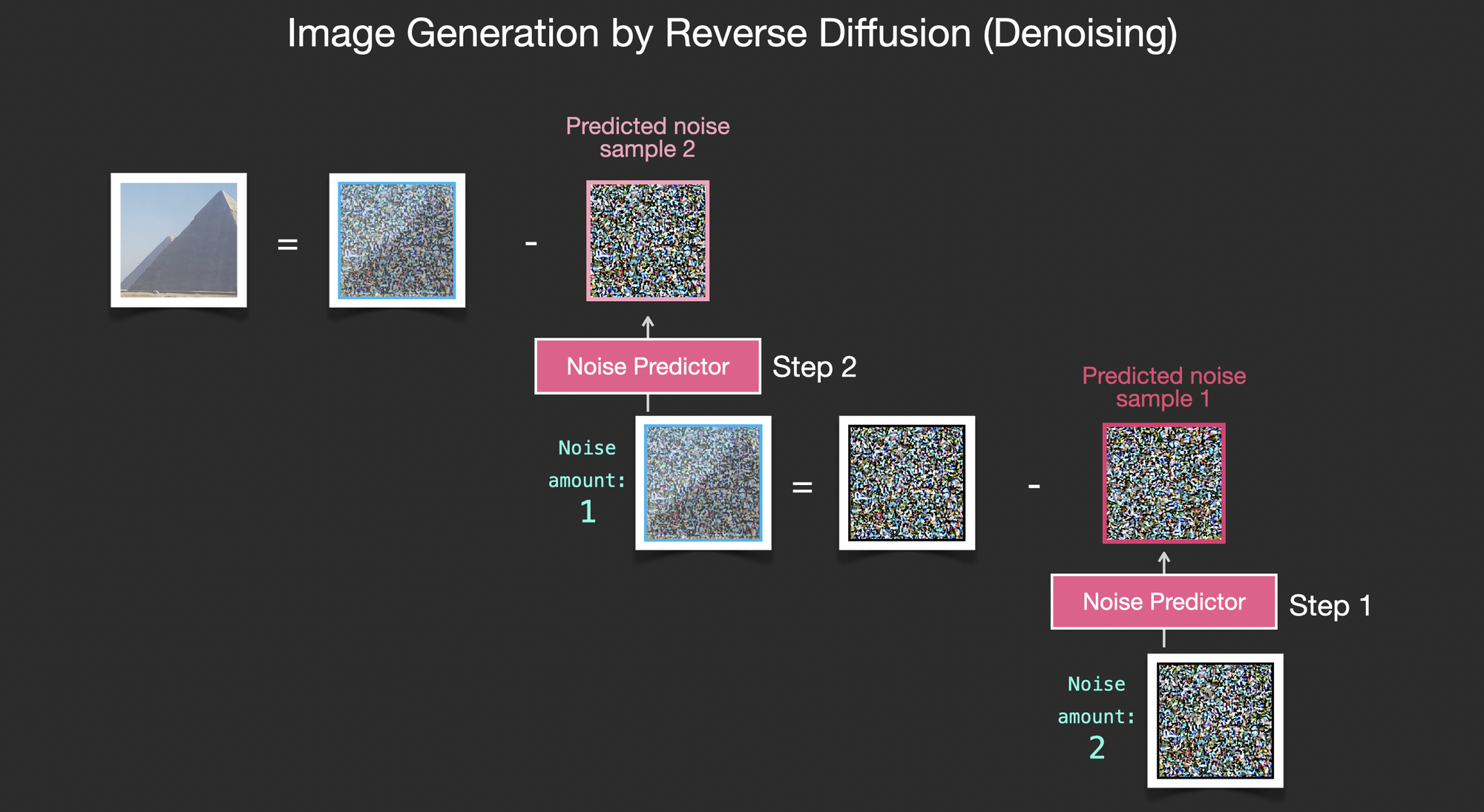
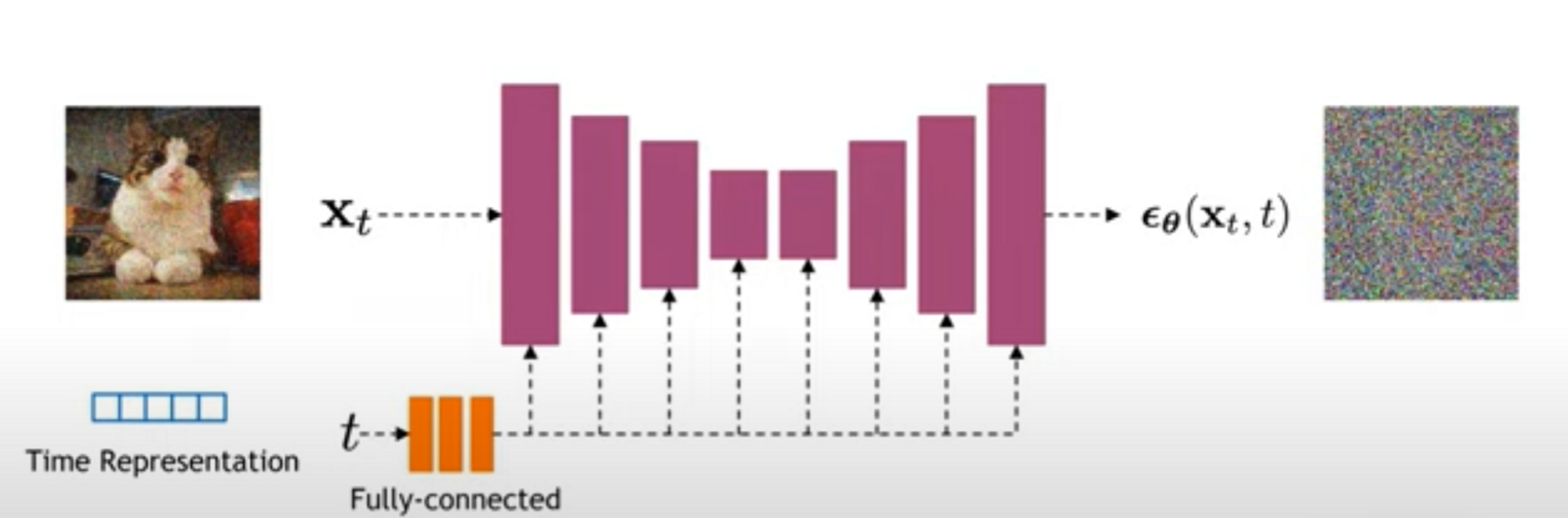
실제로는, "노이즈의 정도"는 곧 "몇 번 노이즈를 씌웠는가"이기 때문에 time step이라고 보통 부른다.

TMI) time step

TMI) time step은 그냥 숫자로 바로 넣는 것이 아니라, 임베딩으로 바뀐 후 한번 해석(FC layer)을 거쳐서 들어간다.

 

❓ 왜 노이즈를 한번에 안빼고?

"한방에 노이즈에서 이미지로 가는 모델을 학습시키는 것은 어려우나,

이것을 여러 단계로 나누어서 점진적으로 denoising을 하는 것은 상대적으로 학습시키기 쉽다!”라고 직관적으로 이해하면 된다.

 

TMI) 좀 더 디테일한 설명, 이론

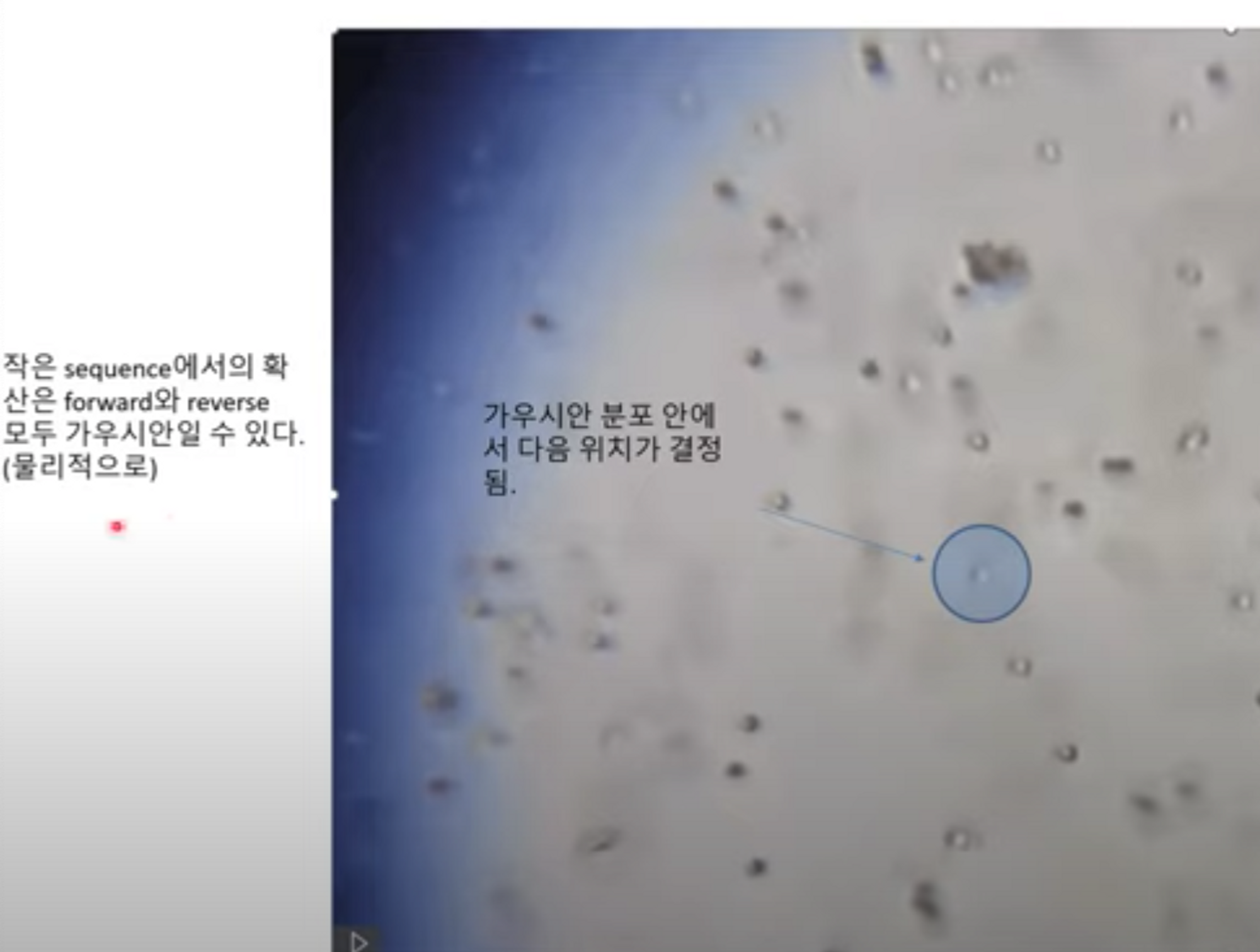
• 아래 이미지에서 설명하는 바와 같이, “확산”이 이뤄질 때, 아주 작은 시간 뒤에 해당 입자가 어디로 이동하는지는, 현재 위치를 평균으로 한 “가우시안 분포”안에서 결정이 된다.
• 또한, 그것의 역과정 또한 가우시안일 수 있게 된다.
• 이런 식으로 ‘이전의 값’에 의해서만 영향을 받는 확률 과정을 markov chain이라고 하며, 사실 이러한 배경이 있기 때문에 (노이즈가 낀 이미지; $$ z_{t-1}, time step $$ )를 입력으로 (노이즈가 빠진 이미지; $$  z_{t})$$ 를 예측할 수 있는 것이다.

From Youtube - https://youtu.be/uFoGaIVHfoE

 

다만, Stable Diffusion은 입력한 텍스트(이하 프롬프트)에 맞는 이미지를 만들어내야 하므로,

U-Net은, time step만이 아니라 프롬프트 정보 또한 입력으로 받는다. 

 

TMI) 프롬프트를 이미지에 반영하는 방법

• 받은 텍스트 정보를 이미지의 특정 영역과 연관 짓게 하기 위해서 U-Net 내부에는 Cross-Attention이 들어가있다.
• cross attention: “[A] [cat] [in] [the] [forest]”라는 프롬프트가 있으면, 이미지(정확히 말하자면 latent)의 영역들과 프롬프트의 각 토큰과의 연관성을 계산하는 방식. (e.g. 배경영역에는 forest에 대한 attention 값이 높을 것이고, 고양이 객체에는 cat에 대한 attention 값이 높을 것)

예시 이미지. 숲속의 고양이 (A cat in the forest)

 

🥚🤐 Image Encoder, Image Decoder

이름 그대로 code(이하 latent, 이미지에 대한 정보가 압축된 숫자들(벡터))로 만들고, 그것을 다시 해석하는 모델.

Latent, Code에 대해서 정리한 글: https://heung-heung.tistory.com/entry/Low-Manifold-Theory-Manifold-Hypothesis-Latent-Encoder-Docoder-Embedding%EC%97%90-%EA%B4%80%ED%95%9C-%EA%B8%80

Low Manifold Theory, Manifold Hypothesis (Latent, Encoder, Docoder, Embedding에 관한 글)

 

그냥 간단하게, 이미지 압축! 압축해제!의 역할이다.

 

TMI) 논문에서는 f = {1, 2, 4, 8, 16, 32}배로 줄어들게 압축 시도했으며
(e.g. f=4, 256x256 ⇒ 64x64), 4와 8정도 수준에서 가장 적절한 효율과 퀄리티 간의 타협점을 찾았다고 함.

 

압축 시의 장점: 불필요한 연산량이 줄어든다. (기존에는 5만장 만드는데 5일 걸리기도 함.)

 

TMI) 압축시의 장점

• 기존에는, nosing-denosing이 이미지에 대해서 직접적으로 적용이 되었음.
  → U-Net이 이미지에서 의미없는 정보들을 제거/무시하는 능력도 가져야했고, 불필요하게 사이즈가 컸음.
  → 과도한 컴퓨터 연산량 요구. 50000장 생성하는데에 5일 걸리는 모델도 있었음.
  → 혹은 작은 이미지에 대한 diffusion 모델을 학습하고, 별도로 SR을 통해 고해상도 이미지를 만들어 내기도 함.
  (e.g. Google의 Imagen, 256까지만 만들고 1024로 SR.)
  → 어찌되었건 최종이미지 사이즈가 커지면 커질수록 더욱 문제가 됨.
  → 덕분에 파라미터의 수가 40억개🙀
  → SD에서는 encoding 덕분에 14억개로 3분의 1 가량으로 줄어듬.
• Encoder 파트는 고정시켜놓고, Denoiser만 갈아끼울 수도 있음.
  → 다양한 실험이 가능해지고, 이미지 복원력은 decoder가 맡고 생성력은 denoiser가 맡는 역할의 분리가 이뤄짐.
  (원래 DDPM 등에서는 reweighted variational objective 사용.)
• 1차원으로의 압축에 비해서 나은 점: 2차원의 latent를 이용하기에 denoiser가 이미지에 대한 inductive bias(귀납적 편향)가 담긴 U-Net구조(2d Conv, 사실상 reweighted)를 활용할 수 있음.

DDPM 논문 캡처본. time step이 작을 때(노이즈가 거의 없을 때) 노이즈를 제거하는 일보다 time step이 클 때(완전한 노이즈에 가까울 때)의 denoising이 더 어렵기 때문에 reweight를 했다고 서술함.

🤖 CLIP

우리는 Text-To-Image를 원하기 때문에, denoising시에 조건으로 줄 “해석된 텍스트”가 필요하다.
(컴퓨터의 입장에서 해석된, 즉 숫자들로 표현된 벡터.)

 

텍스트를 해석하는 모델은 CLIP이며, 이 모델은 “이미지”와 그에 대한 설명글인 “캡션”의 pair 데이터셋에 의해서 학습된다.

위에가 이미지, 이 글이 캡션

• 입력받은 이미지와 텍스트(캡션) 간의 유사도를 높이는 방향으로 학습한다.
• 모델에게는 이미지와 캡션이 일치하는 postive case와, 일치하지 않는 negative case를 모두 보여주며,
  1과 0의 라벨로 학습을 시킨다.
• 그 결과로 CLIP을 거친 개의 이미지와 “a picture of dog”의 latent는 매우 유사한 값이 나올 것이다.
  → 때문에 SD에서 Text-To-Image와 Image-To-Image가 둘다 가능한 것.

 

⭐️마무리

모델의 대략적인 구조도. 빨간색 ➡️ 노란색 ➡️ 파란색 순서로 설명했다.

자 다시 위 그림을 보자.

우리가 "paradise cosmic beach"라는 프롬프트을 입력하면,

CLIP이라는 모델은, 우리가 입력한 프롬프트를 해석하고, 그게  U-Net에 들어간다.

U-Net은 노이즈와, Time step(노이즈의 정도), 프롬프트를 입력받아서, "노이즈가 빠진 이미지"를 예측한다.

그것을 반복하다 보면(위 그림에서는 50번), "노이즈 없는 이미지(사실 Latent)"가 만들어지고,

이것을 압축해제(Decoder로)만 하면, 이미지가 나오는 것이다!

 

 

이 글이 여러분에게 도움이 되었기를 바라며,

아래에 내가 인용한 이미지들에 대한 출처를 남긴다.

 

유용한 Diffusion 설명 영상: https://youtu.be/uFoGaIVHfoE

그림으로 설명한 Diffusion: https://jalammar.github.io/illustrated-stable-diffusion/